متوازي المستطيلات يُعَدّ أحد الأشكال الهندسية الفراغية التي تكثر دراستها في الرياضيات والهندسة، ويتميّز ببنيته المنتظمة وأبعاده المحددة التي تمنحه ثباتاً وشكلاً واضح المعالم، وهو جسم ثلاثي الأبعاد تتقابل فيه كلّ وجهين بشكل مستطيل، وتتساوى الأوجه المتقابلة في الشكل والمساحة، ويحتل هذا الشكل أهمية كبيرة في التطبيقات العملية كالحسابات الهندسية والبنائية وقياس الأحجام والمساحات في الحياة اليومية.
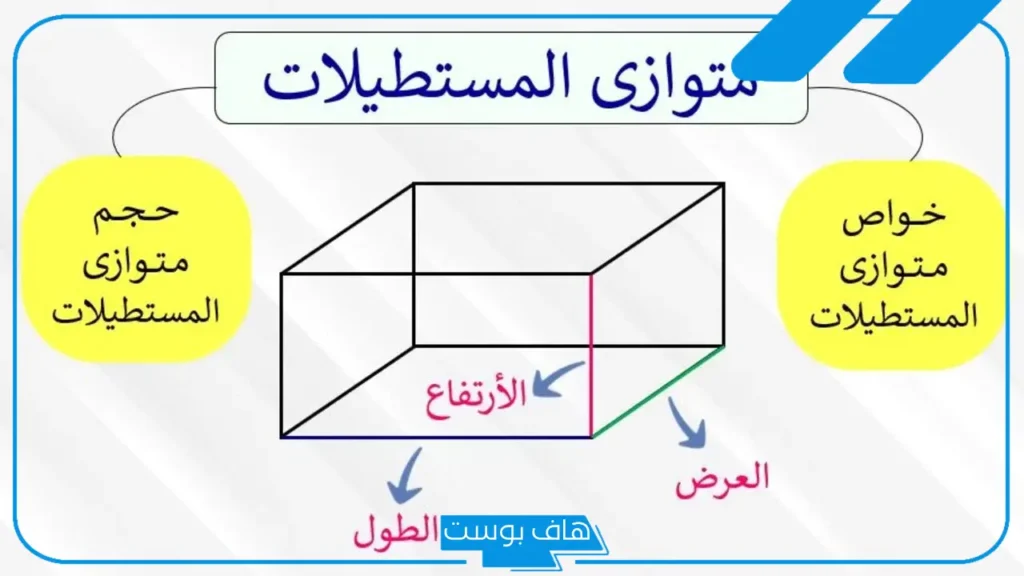
معلومات عن متوازي المستطيلات
- عدد أبعاده: يتكوّن متوازي المستطيلات من ثلاثة أبعاد أساسية: الطول، والعرض، والارتفاع، وهي التي تحدد حجمه وشكله.
- عدد أوجهه: له ستة أوجه، كل وجه منها على شكل مستطيل، وتكون الأوجه المتقابلة متساوية في المساحة.
- عدد أحرفه: يحتوي على 12 حرفاً، تتوزع بحيث يشكّل كل أربعة أحرف متوازية مجموعة من الأبعاد الثلاثة.
- عدد رؤوسه: يتكوّن من 8 رؤوس، تلتقي عند كل رأس ثلاثة أحرف تمثل أبعاده.
- شكل أوجهه: جميع الأوجه مستطيلات، إلا أن مقاييسها قد تختلف تبعاً لأبعاد الشكل.
حجم متوازي المستطيلات
- يُحسَب حجم متوازي المستطيلات بضرب أبعاده الثلاثة: الطول في العرض في الارتفاع.
ويُعبّر الحجم عن مقدار الحيّز الذي يشغله الشكل في الفضاء، وتبرز أهمية هذا القانون في عمليات القياس والتخزين والشحن، حيث يسهّل معرفة السعة الكلية لأي جسم يشبه متوازي المستطيلات، فعندما تكون الأبعاد معروفة، يصبح إيجاد الحجم عملية مباشرة تُستخدم فيها الوحدات المكعّبة مثل سنتيمتر مكعب أو متر مكعب.
قاعدة متوازي المستطيلات
- قاعدة متوازي المستطيلات هي القاعدة ضرب الارتفاع المتعلق بها.
وتعرف المساحة التي تغطي أحد أوجهه المستطيلة، وغالباً ما يُطلَق عليها اسم مساحة القاعدة، وتحسب مساحة القاعدة بضرب الطول في العرض، وهما بعدا الوجه السفلي أو أي وجه يُعدّ قاعدة، وتُعدّ مساحة القاعدة مهمة لأنها تُستخدم أحياناً في حساب الحجم من خلال ضربها في الارتفاع، مثال: إذا كان طول القاعدة 5 سم، وعرضها 3 سم، فإن مساحة القاعدة تساوي:
5 × 3 = 15 سم².
شكل متوازي المستطيلات
- شكل ثلاثي الأبعاد: يُمثّل جسماً مجسّماً له طول وعرض وارتفاع.
- أوجه مستطيلة: جميع الأوجه على هيئة مستطيلات، متقابلة ومتماثلة.
- حواف مستقيمة: يتكوّن من 12 حرفاً مستقيمة تشكّل إطار الشكل.
- زوايا قائمة: كل الزوايا فيه قائمة (90 درجة) عند الالتقاء بين الأحرف.
عدد رؤوس متوازي المستطيلات
يتكوّن متوازي المستطيلات من ثمانية رؤوس، وهي النقاط التي تلتقي عندها ثلاثة أحرف، وتمثل هذه الرؤوس زوايا الشكل، وجميعها زوايا قائمة، وتُعدّ معرفة عدد الرؤوس مهمة في التمثيل الهندسي وفي فهم تركيبة الشكل، حيث يمكن رسمه أو نمذجته بناءً على تحديد هذه النقاط الثمانية التي تُعطي الشكل بنيته الفراغية المتكاملة.
مساحة متوازي المستطيلات
تحسب المساحة الكلية لمتوازي المستطيلات عن طريق إيجاد مساحات أوجهه الستة. ولأن الأوجه المتقابلة متساوية، يمكن استخدام الصيغة التالية:
- المساحة الكلية = 2 × (الطول × العرض + الطول × الارتفاع + العرض × الارتفاع).
وتعبّر هذه المساحة عن مجموع المساحات التي تغطي السطح الخارجي للشكل، وتفيد هذه العملية في تصميم الأغلفة، وتغليف الصناديق، وفي التطبيقات الصناعية التي تتطلب معرفة مساحة السطح الذي يحتاج لطلاء أو تغليف.
والآن يبلغ ختام المقال الذي كان يحمل عنوان متوازي المستطيلات، يبقى من أبرز المجسّمات الهندسية التي تجمع بين البساطة والدقة، وتدخل خصائصه في شتى مجالات الحياة التعليمية والعملية، فمعرفة أبعاده، ومساحاته، وحجمه، تمنحنا قدرة واسعة على التعامل مع التطبيقات الهندسية المختلفة، ويظل هذا الشكل نموذجاً واضحاً لفهم أساسيات الهندسة الفراغية، ومظهراً من مظاهر التنظيم الهندسي في الطبيعة والصناعة.